Möglichkeiten und Grenzen der Losgrößenoptimierung
Dr. G.-A. Kemmner1
Losgrößenverfahren zur Kostenreduktion bei der Lagerhaltung und Beschaffung eines bestimmten Guts sind für Entscheider in der Logistik ein wichtiges Thema. Um die Potenziale jedoch umfassend ausschöpfen zu können, müssen Anwender auch die Grenzen der Losgrößenverfahren kennen und sich bewusst sein, dass man mit den Verfahren nicht alle gesamtbetrieblichen Interdependenzen berücksichtigen kann. Für den Einsatz an der strategisch richtigen Stelle ist deshalb entsprechende Methodenkompetenz über die Supply Chain hinweg gefragt.
Mit Losgrößenverfahren soll ein Optimum zwischen Lagerhaltungskosten und Beschaffungskosten berechnet werden, um so die Gesamtkosten der Supply Chain zu minimieren. Das Problem dabei ist jedoch, dass eine Losgrößenentscheidung, z. B. für einen spezifischen Wertschöpfungsschritt in der Produktion, nicht zwangsläufig für das Gesamtoptimum der Supply Chain förderlich sein muss. Daher ist es unerlässlich, mögliche Interdependenzen zwischen einzelnen Gütern im Vorfeld zu analysieren.
Kostenarten bei der Losgrößenoptimierung
Die Grundlage aller Losgrößenberechnungen bildet konsequenterweise die Ermittlung der relevanten Kosten, wobei zwei gegenläufig reagierende Kostenarten zu berücksichtigen sind: Die Lagerhaltungskosten und die Beschaffungskosten. Die Lagerhaltungskosten setzen sich zusammen aus den Zinsen des gebundenen Kapitals sowie Kosten für Alterung und Verschleiß, Verlust und Bruch, Transport und Handling innerhalb des Lagers, Lagerung und Abschreibung sowie Lagerverwaltung und Versicherung.
Zu den Beschaffungskosten der Eigenoder Fremdfertigung zählen vor allem Bestellkosten, Rabatte, Boni, Skonti, Zusatzkosten bei ungünstigen Bestell- oder Fertigungsmengen, Transport-, Versicherungsund Verpackungskosten sowie Auftragsbearbeitungskosten und die Rüstkosten.
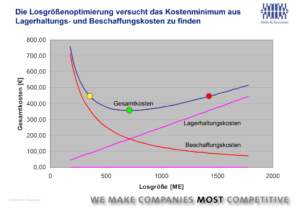
Größere Losgrößen in der Beschaffung führen zu höheren Beständen und damit höheren Lagerhaltungskosten. Diese steigen i. Allg. proportional zur Losgröße, während die Beschaffungskosten degressiv fallen (Bild 1). Um diese unterschiedlichen Kostenkurven zu einem Gesamtoptimum zu bringen, wurden und werden unterschiedliche Verfahren entwickelt, die man in der Summe unter Losgrößenverfahren zusammenfasst.
Die wichtigsten Losgrößenverfahren
Bei den Losgrößenverfahren lässt sich zwischen statischen Verfahren und dynamischen Verfahren unterscheiden. Statische Verfahren (wie das Andler-Verfahren) fokussieren nur die komplette Bedarfsmenge innerhalb eines Betrachtungszeitraums und sind damit nur überschlägige Berechnungsverfahren. In die dynamischen Verfahren bzw. periodischen Losgrößenverfahren fließen hingegen Bedarfe über einen gewissen Zeitraum hinweg ein. Damit sind diese Verfahren grundsätzlich nachfrageorientierter und können sich so veränderten Bedarfen anpassen. Zu dieser Gruppe von Verfahren gehören:
- Das Wagner-Whitin-Verfahren,
- das Part-Period-Verfahren (Stück-Perioden-Ausgleichsverfahren),
- das Stückkosten-Verfahren (Verfahren dergleitenden wirtschaftlichen Losgröße) sowie
- das Groff-Verfahren und
- das Silver-Meal-Verfahren.
Die Anzahl unterschiedlicher Verfahren erklärt sich daraus, dass bisher niemand in einer Formel die komplexe Realität wirklich exakt abbilden konnte. Insofern sind alle Losgrößenverfahren nur Näherungslösungen. Einige sind jedoch näher am Optimum als andere. Die genannten Verfahren muss man deshalb sehr genau verstehen, um sie nutzbringend anwenden zu können.
Andler ist vielfach zu ungenau
Die von Kurt Andler entwickelte Formel ermittelt das Minimum der Gesamtkostenkurve (Bild 1), auf Grundlage der Annahme, dass die Gesamtbedarfsmenge eines Artikels in einem Planungszeitraum, z. B. ein Jahr, bekannt ist. Aus den Lagerhaltungskosten und den Beschaffungskosten leitet die Formel eine ideale Losgröße ab, die über den Planungszeitraum konstant bleibt.
Problematisch dabei ist, dass in der Praxis Produktions- oder Bestellbedarfe über einen Planungszeitraum nicht konstant sind, sondern unregelmäßig aufeinander folgen und unterschiedlich hoch ausfallen (Bild 2).
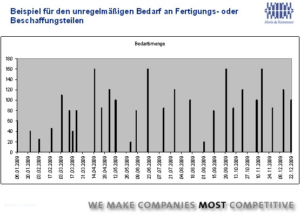
Wagner-Within ist sehr exakt
Das Wagner-Within-Losgrößenberechnungsverfahren berücksichtigt, dass mit der Entscheidung über eine erste Losgröße im Betrachtungszeitraum automatisch auch der Spielraum für die Gestaltung der zeitlich nachfolgenden Losgrößen eingeschränkt wird. Das Verfahren ermittelt eine Folge von Losen unterschiedlicher Größe und Zeitabständen, die die Gesamtkosten bei einer einstufigen Einproduktfertigung ohne Kapazitätsbegrenzung minimiert.
Allerdings wird das Wagner-Whitin-Verfahren für Losgrößen für unzählige Produkte sehr komplex. Aus diesem Grund wurden Näherungsverfahren mit einfacheren Rechenmethoden entwickelt (Part-Period-Verfahren, Silver-Meal-Verfahren, Groff-Verfahren), die Vereinfachungen vornehmen und so das Kostenoptimum auch bei unterschiedlichen Losgrößen ermitteln. Die Abweichungen vom exakt rechnenden Wagner-Whitin-Verfahren können dabei sehr deutlich ausfallen (Bild 3).
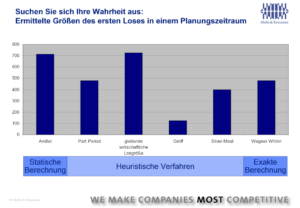
Viele Standard-ERP-Systeme verwenden das Wagner-Whitin-Verfahren nicht. Mithilfe von Add-on-Lösungen lassen sich die Wertschöpfungsketten allerdings auch mit diesem sehr genaue Ergebnisse liefernden Verfahren optimieren.
Begrenzte Maschinenkapazität beeinflusst Formel
Allen genannten Verfahren ist gemeinsam, dass sie das Zusammen- bzw. Gegeneinanderwirken von Lagerhaltungskosten und Beschaffungskosten in einer einstufigen Einproduktfertigung ohne Kapazitätsbegrenzung beschreiben. Doch eigentlich tritt die Frage nach einer Losgröße erst auf, wenn mehr als ein Produkt gefertigt wird. Auch wenn mehrere Produkte auf einer Anlage gefertigt werden, stimmen die dem Verfahren zugrundeliegenden Formeln, sofern sich die Losgrößen der beiden Produkte nicht gegenseitig durch eine begrenzte Maschinenkapazität beeinflussen. Doch in der Praxis ist die Maschinenkapazität häufig begrenzt. Es gibt zwar Losgrößenoptimierungsverfahren, die eine ganze Prozesskette berücksichtigen. Doch will man realistischerweise in die Analysen auch noch einbeziehen, dass die Kapazitäten auf den einzelnen Fertigungsstufen begrenzt sind, lässt sich die Realität nicht mehr vollständig mit all den gegebenen Interdependenzen und Limitierungen durchrechnen.
In der Beschaffung sieht es ähnlich aus. Auch hier lässt sich häufig keine isolierte Losgrößenbetrachtung bei einem einzelnen Produkt anstellen. Zum einen können sich mehrere verschiedene Produkte Beschaffungskosten „teilen”: Beispielhaft genannt sei ein Lkw, der mit mehreren Produkten beladen werden kann. Zum anderen geht es häufig darum, die Kapazität der Lkw-Ladefläche möglichst vollständig auszunutzen, um die Transportkosten zu minimieren. Mehrere Produkte werden also gezielt zusammen bestellt und beeinflussen sich somit hinsichtlich ihrer Bestellmengen gegenseitig. Mit der vermeintlich „optimalen” Bestellmenge eines Produkts wird folglich der Spielraum der Bestellmengen für die anderen Produkte automatisch eingeschränkt.
Fazit
In der Praxis sind bei der Berechnung von Losgrößen etliche Details zu berücksichtigen. Der mit der Aufgabe der Losgrößenoptimierung Betraute muss daher die einzelnen Verfahren und ihre Eigenschaften genau verstehen. Losgrößenoptimierung ist nicht die einfache Supply-Chain-Optimierung mithilfe von Formelsätzen, die vom PC durchgerechnet werden. Vielmehr ist die Losgrößenoptimierung eine Betätigung für Spezialisten, die die Anwendung der Methode in den richtigen Kontext setzen und die Kostenberechnungen so durchführen, dass die Ergebnisse genau sind.

