Sieben Hürden überwinden
Produktion in passender Losgröße
In der Praxis werden Losgrößenverfahren zur Kostenreduktion von Lagerhaltung sowie Beschaffung und Fertigung nur selten eingesetzt. Dabei lässt sich so oft eine Menge Geld sparen. Um das Potenzial der Verfahren ausschöpfen zu können, müssen Anwender um die Grenzen der Ansätze wissen − denn alle betrieblichen Interdependenzen können sie nicht berücksichtigen. Für den punktgenauen Einsatz ist deshalb Methodenkompetenz über die gesamte Lieferkette hinweg gefragt.
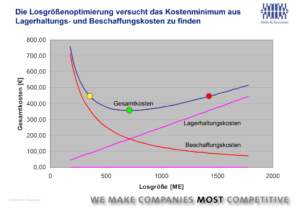Mit wirtschaftlichen Losgrößenverfahren sollen die minimalen Gesamtkosten aus Lagerhaltungskosten einerseits und Beschaffungs- beziehungsweise Rüstkosten andererseits berechnet werden, um so die Gesamtkosten der Wertschöpfungskette zu minimieren. Größere Losgrößen in der Beschaffung und Fertigung führen zu höheren Beständen und damit zu höheren Lagerhaltungskosten. Diese steigen im Allgemeinen proportional zur Losgröße, während die Beschaffungskosten umgekehrt proportional fallen (siehe Abbildung oben). Dort, wo sich die beiden Kostenkurven schneiden, liegt das gesuchte Minimum der Gesamtkosten.
Kostenarten bei der Losgrößenoptimierung
Die Grundlage aller wirtschaftlichen Losgrößen-Berechnungen bildet dabei konsequenterweise die Ermittlung der Lagerhaltungskosten sowie der Beschaffungs- und Rüstkosten. Die Lagerhaltungskosten setzen sich zusammen aus den Zinsen des gebundenen Kapitals sowie aus Kosten für Alterung und Verschleiß, Verlust und Bruch, Transport und Handling innerhalb des Lagers, Lagerung und Abschreibung sowie Lagerverwaltung und Versicherung. Zu den Beschaffungskosten können zählen: Bestellkosten, Rabatte, Boni, Skonti, Zusatzkosten bei ungünstigen Bestell- oder Fertigungsmengen, Transport-, Versicherungs- und Verpackungskosten, Auftragsbearbeitungskosten. Etwas weniger Kostenarten berücksichtigt man meist bei den Rüstkosten. In praktisch allen Fällen handelt es sich um kalkulatorische Kosten und so muss betriebsspezifisch und aus unternehmerischer Perspektive festgelegt werden, welche kalkulatorischen Kosten in welcher Höhe anzusetzen sind. Auf dem Weg zu wirtschaftlichen Losgrößen gilt es nun, fünf Hürden erfolgreich zu überwinden. Die erste Hürde stellt die Berücksichtigung der richtigen Kostenarten und deren Höhe dar.
Der klassische ‘Andler’ greift meist zu kurz
Bei den wirtschaftlichen Losgrößenverfahren unterscheidet man gewöhnlich zwischen statischen Verfahren und dynamischen Verfahren. Das zentrale statische Verfahren stellt das Andler-Verfahren dar. Die von Kurt Andler 1927 entwickelte Formel ermittelt das Minimum der Gesamtkostenkurve auf Grundlage der Annahme, dass die Gesamtbedarfsmenge eines Artikels in einem Planungszeitraum, zum Beispiel ein Jahr, bekannt ist. Die Formel leitet aus Lagerhaltungskosten und Beschaffungskosten eine wirtschaftliche Losgröße ab, die über den Planungszeitraum konstant bleibt und in einem konstanten Rhythmus abgerufen werden muss, damit sich tatsächlich die angestrebten minimalen Kosten ergeben. Das Problem: In der Praxis sind Produktions- oder Bestellbedarfe über einen Planungszeitraum nicht konstant, sondern folgen unregelmäßig aufeinander und fallen unterschiedlich hoch aus. Besonders deutlich ist dies bei den Planbedarfen einer plangesteuerten Disposition. Aber auch beim Meldebestandsverfahren ist die Bedarfsmenge zumeist nicht regelmäßig, wie ein Blick in Vergangenheitsdaten zeigt. Der Herausforderung unregelmäßiger Bedarfe versuchen die dynamischen wirtschaftlichen Losgrößenverfahren zu begegnen, indem sie sich an der realen Bedarfssituation orientieren.
Zu den verbreitetsten Verfahren dieser Gruppe gehören:
- das Part-Period-Verfahren oder Stück-Perioden-Ausgleichsverfahren,
- das Stückkosten-Verfahren oder Verfahren der gleitenden wirtschaftlichen Losgröße,
- das Groff-Verfahren,
- das Silver-Meal-Verfahren und
- das Wagner-Whitin-Verfahren.
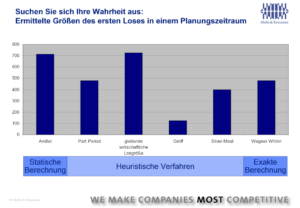
Alle aufgeführten Verfahren − mit Ausnahme des Wagner-Whitin-Verfahrens − sind dabei als Näherungsverfahren zu verstehen, die sequenziell, Bestellung für Bestellung, aus der Bedarfszeitreihe wirtschaftliche Lose ‘zusammenraffen’. Lediglich das Wagner-Whitin-Verfahren ermittelt das Optimum über alle Bestellmengen und Fertigungslosgrößen des Planungszeitraumes.
Der Wagner-Within-Ansatz ist sehr exakt
Das Wagner-Whitin-Verfahren wurde bereits 1958 entwickelt. Da es für die ersten Materialwirtschaftsprogramme zu rechenintensiv und von Hand schon gar nicht anzuwenden war, wurden in den folgenden Jahren die oben angeführten Näherungsverfahren konzipiert. Die Abweichungen der Näherungsverfahren vom exakt rechnenden Wagner-Whitin-Verfahren können dabei sehr deutlich ausfallen, wie sich oben auf der Abbildung erkennen lässt. Die meisten ERP-Systeme unterstützen das Wagner-Whitin-Verfahren nicht. In vielen Add-On-Systemen zur Disposition steht es jedoch zur Verfügung. In der Praxis kann das Wagner-Whitin-Verfahren seinen theoretischen Vorsprung gegenüber den Näherungsverfahren oder dem Andler-Verfahren nicht immer ausspielen, da sich die Struktur der Planbedarfe über den Planungshorizont von MRP-Lauf zu MPR-Lauf verändert und das Verfahren sozusagen hinter einem ‘moving Target’ herläuft. Trotzdem bewältigen Unternehmen die zweite Hürde der wirtschaftlichen Losgrößenoptimierung meist am besten, wenn sie bei plangesteuerter Disposition auf das Wagner-Whitin-Verfahren setzen. Welche wirtschaftlichen Vorteile sich durch den Einsatz welches wirtschaftlichen Losgrößenverfahrens erreichen lassen, kann mit Simulationssystemen ermittelt werden, ehe man die wirtschaftlichen Losgrößenverfahren in der Praxis einsetzt.
Auf diese Weise lassen sich auch die Artikel ermitteln, bei denen sich die größten wirtschaftlichen Vorteile ergeben. Durch eine solche Simulation lässt sich die dritte Hürde der wirtschaftlichen Losgrößenoptimierung nehmen, nämlich dort anzusetzen, wo die größten wirtschaftlichen Effekte erzielt werden. Um Losgrößenverfahren in der Praxis nutzbringend einsetzen zu können, müssen noch weitere Aspekte berücksichtigt werden: Alle klassischen wirtschaftlichen Losgrößenverfahren betrachten eine einstufige Einproduktfertigung mit unbegrenzter Kapazität.
Bei der Berechnung der Losgröße wird nicht beachtet,
- dass meist mehrere Produkte über eine einzelne Fertigungskapazität laufen und
- dass die wirtschaftliche Losgröße auf einer Wertschöpfungsstufe negative Auswirkungen auf davor oder dahinter liegende Wertschöpfungsstufen haben können.
Besonders in der Fertigung, aber teilweise auch in der Beschaffung, müssen diese Randbedingungen auch in die Gestaltung der Losgrößen einbezogen werden. Führt die Kombination wirtschaftlicher Losgrößen auf einer Fertigungskapazität zu Kapazitätsengpässen, müssen die Losgrößen soweit erhöht werden, dass die Fertigungskapazität wieder ausreicht. In der Beschaffung hingegen kann es erforderlich sein, wirtschaftliche Losgrößen zu verringern, damit alle Bedarfe in die verfügbare Transporteinheit passen.
Nach fünf Hürden kommt die Kür
Die vierte Hürde bei der wirtschaftlichen Losgrößenoptimierung stellt deshalb der Kapazitätsabgleich dar. Auch kann es in einer Kette aufeinanderfolgender Dispositionsstufen erforderlich sein, Losgrößen aufeinander abzustimmen. Die richtigen Losgrößenkompromisse zwischen Dispositionsstufen zu machen, stellt die fünfte Hürde dar, die es zu meistern gilt. Diese fünf Hürden stecken gewissermaßen den Pflichtparcours für Losgrößenoptimierer ab. Hinzu kommt die Kür: als sechste Hürde kann die Aufteilung in gleichmäßige Arbeitsinhalte verstanden werden. Als siebte Hürde lassen sich losgrößenabhängige Durchlaufzeiten berücksichtigen, denn auch Umlaufbestände in der Produktion können signifikante Lagerhaltungskosten verursachen.
Eine Formel reicht nicht aus
In der Praxis scheuen viele Unternehmen den Aufwand, wirtschaftliche Losgrößen richtig einzustellen, wenn sie erst einmal erkannt haben, dass das einfache Anwenden einer Formel nicht genügt. Damit vergeben sie jedoch ein beachtliches wirtschaftliches Optimierungspotenzial. Dabei lässt es sich bei strukturiertem Vorgehen, ganzheitlicher Betrachtung und dem Einsatz passender Werkzeuge im Grunde genommen recht einfach bergen.
