Optimale Losgröße: Wirtschaftliche Losgrößenverfahren – wie funktionieren sie überhaupt?
Für die optimale Losgröße werfen wir einen Blick auf wirtschaftliche Losgrößenverfahren. Wirtschaftliche Losgrößenverfahren zur Gesamtkostenreduktion von Lagerhaltung und Beschaffungs- bzw. Rüstkosten bieten ein großes, zumeist ungenutztes Potenzial zur Kostensenkung. Um wirtschaftliche Losgrößenverfahren richtig anwenden zu können, müssen Anwender Prinzip und Grenzen der wirtschaftlichen Losgrößenverfahren verstehen.
Ziele der wirtschaftlichen Losgrößenverfahren bei der Losgrößenoptimierung
Wirtschaftliche Losgrößenverfahren streben an, für einen betrachteten Artikel die Gesamtkosten aus Lagerhaltungskosten einerseits und Beschaffungskosten von Einkaufsartikeln, bzw. Rüstkosten von Eigenfertigungsartikeln andererseits zu minimieren. Dadurch wird ein kleiner wesentlicher Baustein innerhalb der gesamten Supply Chain optimiert, der in der Praxis gerne übersehen wird.
Größere Losgrößen in der Beschaffung oder der Fertigung führen zu höheren Beständen und damit höheren Lagerhaltungskosten. Diese steigen im Allgemeinen proportional zur Losgröße, während die Bestellkosten bzw. Rüstkosten – übergreifend als Losauflagekosten bezeichnet – umgekehrt proportional sinken. Ein einfaches Beispiel: Fallen bei einem Teil für eine Losgröße x dieselben absoluten Transportkosten an, wie für die Losgröße 2x, dann trägt bei doppelt so vielen bestellten Teilen jedes Teil nur noch die Hälfte der Transportkosten.
Wenn bestimmten Kosten proportional zur Losgröße steigen und andere umgekehrt proportional zur Losgröße fallen, dann muss es bei einer bestimmten Losgröße ein Minimum der Gesamtkosten geben (vgl. Abb. 1).
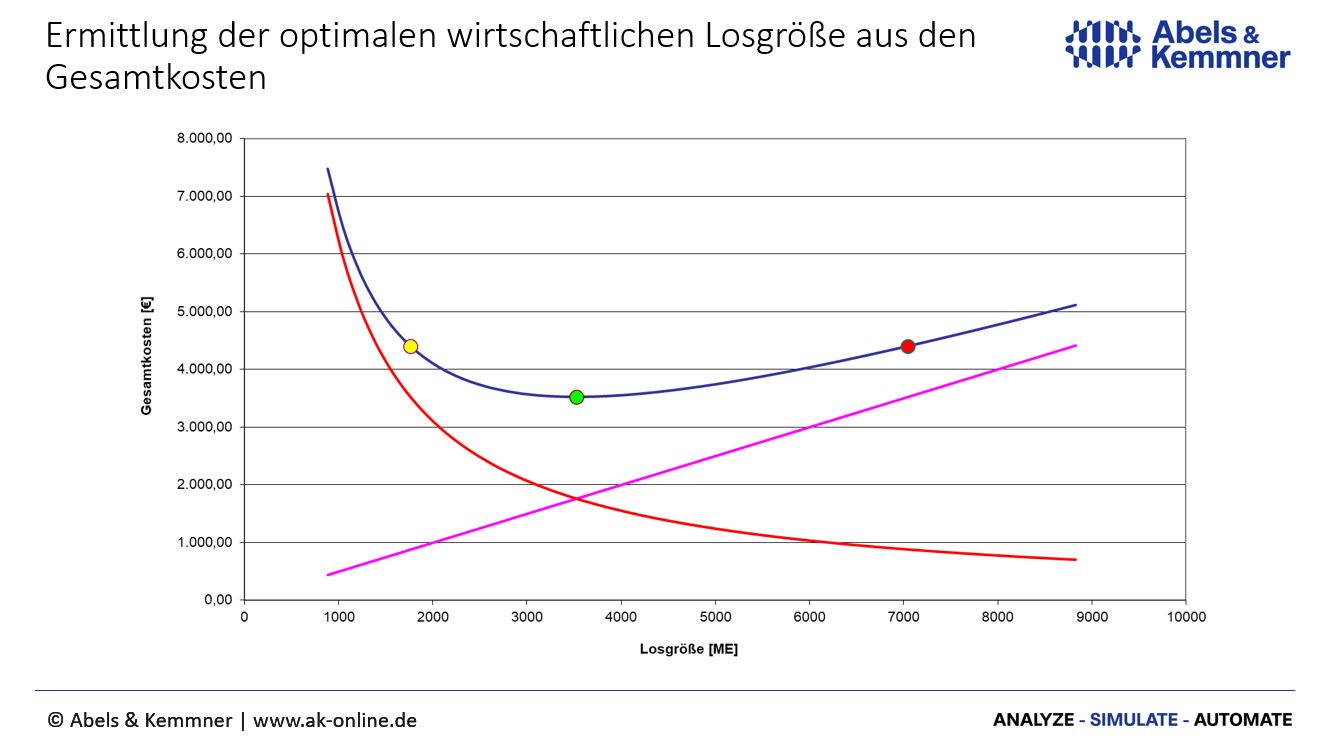
Die klassischen wirtschaftlichen Losgrößenverfahren
Einer der ersten, der den Zusammenhang zwischen Lagerhaltungs- und Losauflagekosten erkannte war Kurt Andler. Er entwickelte 1929 eine Formel zur Berechnung einer wirtschaftlichen Losgröße. Die Andlerformel wird auch heute noch breit angewandt. Bei der Berechnung der optimalen Losgröße ging Andler davon aus, dass die Gesamtbedarfsmenge eines Artikels in einem Planungshorizont, z.B. ein Jahr, bekannt ist. Die Formel leitet nun aus Lagerhaltungskosten einerseits und Beschaffungskosten andererseits die Losgröße ab, mit der immer wieder bestellt werden sollte. Da die Losgröße über den Planungszeitraum konstant bleibt, spricht man auch von einem statischen wirtschaftlichen Losgrößenverfahren.
In der Praxis jedoch, sind Produktions- oder Bestellbedarfe über den Planungshorizont selten gleichmäßig verteilt. Sie folgen vielmehr unregelmäßig aufeinander und fallen unterschiedlich hoch aus (Bild 2). Die entscheidende Antwort, wie man bei „dynamischen“ Bedarfen wirtschaftliche Losgrößen ermittelt gaben zwei Amerikaner bereits 1958. Die Herren Wagner und Whitin entwickelten ein wirtschaftliches Losgrößenverfahren, mit dem dynamische Losgrößen berechnet werden konnten. Diese mathematische Lösung berücksichtigt, dass mit der Entscheidung über eine erste Losgröße im Planungshorizont automatisch auch der Spielraum für die Gestaltung der zeitlich nachfolgenden Losgrößen eingeschränkt wird. Das Wagner-Whitin-Verfahren ermittelt eine Folge von Losen mit unterschiedlicher Größe und unterschiedlichen Zeitabständen, welche die Gesamtkosten minimiert. Das Ergebnis ist eine wissenschaftlich präzise Antwort auf die Frage der richtigen Losgrößen bei einer einstufigen Einprodukt-Fertigung ohne Kapazitätsbegrenzung.
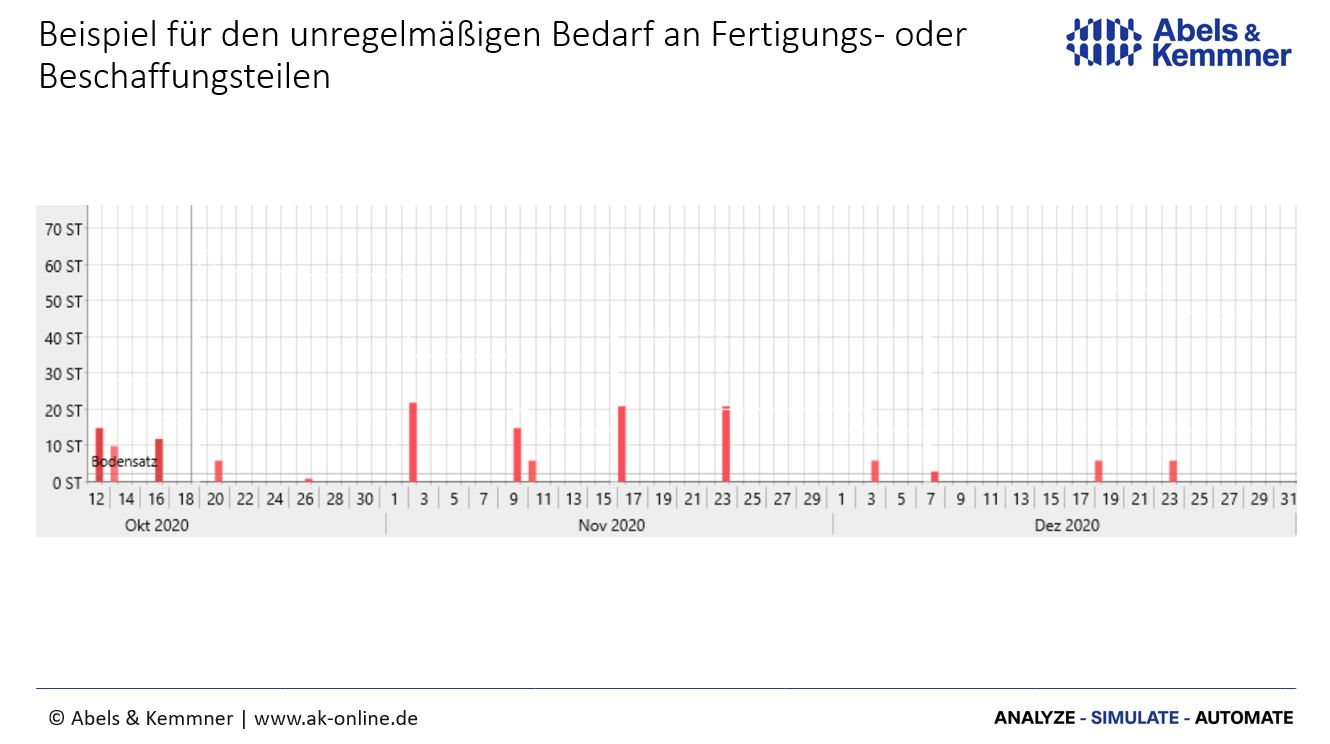
Das Wagner-Whitin-Verfahren war zu aufwändig, um es von Hand oder mit damaligen Rechenmaschinen anzuwenden. So wurden im Laufe der folgenden Jahre Näherungsverfahren entwickelt, die auf Kosten der theoretischen Genauigkeit, mit wenig Rechen- und Speicheraufwand zurechtkommen. 1968 wurden beispielsweise das Part Period-Verfahren und das Verfahren der gleitenden wirtschaftlichen Losgröße, 1973 das nach seinen Entwicklern genannte Silver-Meal-Verfahren und 1979 das Groff-Verfahren vorgestellt. Dies sind die „klassischen“ wirtschaftlichen Losgrößenverfahren, die in vielen ERP-Systemen angeboten werden. Darüber hinaus gibt es noch eine große Anzahl weiterer Verfahren zur Ermittlung optimaler Losgrößen, die in der Praxis bisher wenig Widerhall gefunden haben.
Herausforderung Verfahrensauswahl – optimale Losgröße und wirtschaftliche Losgrößenverfahren
Berechnet man für dieselbe Bedarfssituation eines Artikels wirtschaftliche Losgrößen mit unterschiedlichen Verfahren, weichen die ermittelten Losgrößen meist deutlich voreinander ab. Dies führt in der Praxis zu großen Irritationen.
Die Frage, welches wirtschaftliche Losgrößenverfahren unter realen Bedingungen tatsächlich zu den geringsten Gesamtkosten führt, lässt sich mit modernen leistungsfähigen Softwaretools jedoch beantworten.
Lesen Sie auch Optimale Losgröße – kostengünstigste Losgröße mit wirtschaftlichen Losgrößenverfahren berechnen
Was sind Ihre Erfahrungen zur optimalen Losgröße und wirtschaftlichen Losgrößenverfahren. Schreiben Sie uns!
Auf unserer Wissen-Seite finden Sie weitere hilfreiche Tipps.
