Mehrstufige Bestandsoptimierungsverfahren effizienter gestalten
Die nächste Generation der Multi-Echelon-Inventory-Optimization braucht Künstliche Intelligenz
Multi Echelon bedeutet auf Deutsch “mehrstufig”. Beim Bestandsmanagement sorgt die mehrstufige Optimierung (Multi-Echelon-Inventory-Optimization / MEIO) dafür, dass Bestände mehrerer Standorte und Lagerstufen ganzheitlich optimiert werden. Solche Verfahren sind komplex. Künstliche Intelligenz hilft, diese Komplexität in den Griff zu bekommen.
Inner- und überbetriebliche Supply Chains bestehen aus der Verkettung mehrerer Standorte oder Lagerstufen. In jedem Standort werden verschiedene Artikel bevorratet und zwischen den Standorten gibt es Umlagerungsbeziehungen bzw. Beziehungen, die sich aus den Stücklisten ergeben. Um den Bestand einer einzelnen Lagerstufe richtig zu steuern, sind im Allgemeinen zwei wesentliche Bestandsparameter erforderlich. Zum einen der Grundbestand und zum anderen der Sicherheitsbestand. Der Grundbestand ergibt sich normalerweise aus der Wiederbevorratungszeit mal dem durchschnittlichen täglichen Verbrauch des Artikels.
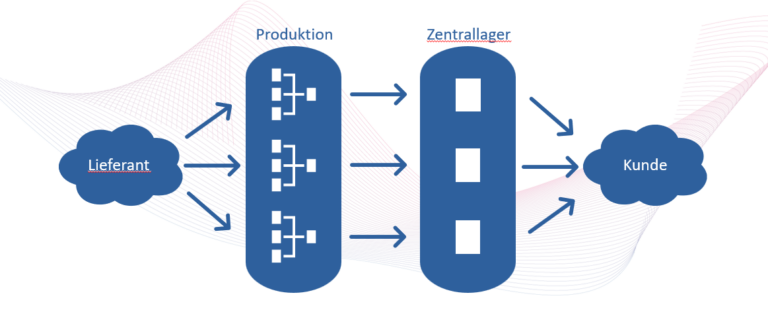
Mehrere Stufen beeinflussen die Lieferbereitschaft
In den Sicherheitsbestand fließen neben der Wiederbeschaffungszeit auch der geforderte Lieferbereitschaftsgrad ein. Je höher der geforderte Lieferbereitschaftsgrad ausfällt, desto höher wird der Sicherheitsbestand. Betrachtet man eine isolierte Lagerstufe alleine, um diese beiden Bestandsparameter zu berechnen, geht man normalerweise davon aus, dass die vorgelagerte Bestandsstufe grundsätzlich lieferfähig ist, also einen Lieferbereitschaftsgrad von 100% aufweist und deshalb immer nach der Wiederbeschaffungszeit die angeforderte Materialmenge liefern kann. Dieses angenommene Konzept ist jedoch nicht realistisch. Typischerweise weist auch die liefernde Bestandsstufe, also die Bestandsstufe, die an die aktuell für die Berechnung ihrer Steuerparameter betrachtete Bestandsstufe liefert, einen Lieferbereitschaftsgrad kleiner 100% aus. Wenn die vorgelegte Bestandsstufe beispielsweise einen Lieferbereitschaftsgrad von 98% aufweist und üblicherweise innerhalb von fünf Tagen liefern kann, bedeutet dies, dass 98% der angeforderten Menge innerhalb von fünf Tagen geliefert werden kann.
Es bleiben 2% an Menge übrig, die nicht innerhalb dieser fünf Tage geliefert werden können, da sie bei der liefernden Bestandsstufe nicht verfügbar sind. Die liefernde Bestandsstufe muss in diesem Falle also auf ihre Vorlieferstufe zurückgreifen. Nehmen wir an, dass die Nachbevorratung von der Vorlieferbestandsstufe sieben Tage benötigt, so lässt sich festhalten, dass in dem genannten Beispiel für 2% der Liefermenge eine Lieferzeit von zwölf Tagen erforderlich ist. Diese Vorlieferstufe ist aber zum Beispiel nur zu 95% lieferfähig. Für 5% der 2% der Liefermenge verlängert sich die Lieferzeit also noch weiter um die Lieferzeit der Vorvorlieferstufe. Dies muss bei der Ermittlung der Bestandssteuerungsparameter der betrachteten Bestandsstufe berücksichtigt werden, um deren geforderte Lieferbereitschaft auch tatsächlich erreichen zu können. In einer innerbetrieblichen Wertschöpfungskette wie in überbetrieblichen Supply Chains haben wir es sehr häufig mit weit mehr als drei Bestandsstufen zu tun, die miteinander verkettet sind, sodass das angeführte Beispiel sich über viele Bestandsstufen hinaus verteilt. Hat man mehrere miteinander verkettete Bestandsstufen und sucht nach dem Bestandsoptimum über alle Bestandsstufen hinweg, stellt sich die Frage, welchen Sicherheitsbestand man bei den verschiedenen Artikeln auf den verschiedenen Bestandsstufen einstellen sollte, um im Endeffekt die Lieferbereitschaft zum Endkunden, die gefordert wird, einhalten und andererseits die Gesamtbestände in der Wertschöpfungskette so gering wie möglich halten zu können.
Optimierungsproblem mit großem Suchraum
Bei dieser Fragestellung handelt es sich um ein Optimierungsproblem mit einem, wie der Mathematiker es nennt, großen Suchraum. Das bedeutet, dass man mit klassischen mathematischen Methoden nicht alle denkbaren Lösungsmöglichkeiten durchprobieren kann. In der Praxis verzichtet man deshalb meist auf die mehrstufige Bestandsoptierung und setzt darauf, für jede Bestandsstufe unabhängig von der Wertschöpfungskette und den anderen Bestandsstufen den Bestand isoliert einzustellen. Etwas weiter geht der Ansatz, anhand von Faustregeln die Bestandsstufen festzulegen, auf denen Sicherheitsbestände gehalten werden sollen, wie dies zum Beispiel beim DDMRP (Demand Driven MRP) der Fall ist. Hierbei spielen Kriterien, wie kritische Komponenten, lange Lieferzeiten oder hohe Nachfrageschwankungen eine Rolle. An den Stellen, an denen mit sich für Sicherheitsbestände entscheidet, wird dann wieder isoliert für die Bestandsstufe und ohne Berücksichtigung der statistischen Versorgungszuverlässigkeit ein Sicherheitsbestand ermittelt.
Die klassische Bestandssteuerung in mehrstufigen Lieferketten fühlt sich zwar aus der Perspektive der Anwender transparent an, da jede Bestandstufe eine kleine Welt für sich darstellt, für die man versucht, einen vernünftigen Kompromiss aus Lieferfähigkeit und Bestandshöhe zu erreichen, führt am Ende der Prozesskette jedoch dazu, dass die Lieferbereitschaft nicht oder nur mit überhöhten Beständen erreicht werden kann.
Dass eine geschickte Verteilung der Bestände auf die verschiedenen Bestandsstufen zu geringeren Beständen und zuverlässigerer Lieferbereitschaft führt, ist theoretisch klar und in einfachen Konstellationen in der Praxis auch erkennbar. Sobald Wertstrom und Supply Chain etwas komplizierter werden, lässt sich die Bestandsverteilung aber nicht mehr berechnen; Zu groß ist die Anzahl der Parameter und exponentiell steigt die Zahl der Lösungen an, die berechnet werden müssten.

Lieferbereitschaft mit geringer Kapitalbindung durch MEIO
Lösen lässt sich die mehrstufige Bestandsoptimierung nur mit Hilfe von mathematischen Optimierungsverfahren. Einen besonders effizienten Ansatz hat die SCT GmbH aus Herzogenrath bei Aachen entwickelt. Ihr neues Multi-Echelon-Inventory-Optimization (MEIO) Verfahren, das nun als Erweiterung in der Software Suite DISKOVER erhältlich ist, optimiert hierzu das Zusammenspiel der einzelnen Wertschöpfungsstufen auf Basis modernster Heuristiken und Metaheuristiken aus dem Bereich der Künstlichen Intelligenz (KI). Ziel ist es, die Bestände über die gesamte Supply Chain hinweg so zu verteilen, dass eine geforderte Lieferbereitschaft an Ende der Supply Chain mit möglichst geringer Kapitalbindung erreicht werden kann.
Das Ergebnis: Höhere Termintreue bei geringeren Beständen über alle Lagerstufen hinweg – mit weniger Planungsaufwand und niedrigeren Kosten. Diese Lösung ist besonders für Unternehmen mit drei oder mehr Lagerstufen von Beschaffung über Produktion bis Distribution relevant.

