Mit Formeln aus der Theorie zum Kostenoptimum in der Praxis?
Losgrößenverfahren zur Gesamtkostenreduktion von Lagerhaltung und Beschaffung eines bestimmten Gutes erscheinen auf den ersten Blick sehr interessant. Um die Potenziale jedoch umfassend ausschöpfen zu können, müssen Anwender auch die Grenzen der Losgrößenverfahren kennen und sich bewusst sein, dass man mit ihnen nicht alle gesamtbetrieblichen Interdependenzen berücksichtigen kann. Für den punktgenauen Einsatz an der strategisch richtigen Stelle ist deshalb entsprechende Methodenkompetenz über die gesamte Supply Chain hinweg gefragt.
Über kaum ein Thema sind so viele Dissertationen geschrieben worden, wie über die Losgrößenoptimierung. Und noch immer erscheinen neue Konzepte und Dissertationen zur Losgrößenberechnung, was zumindest zeigt, dass die Optimierung von Losgrößen in der Theorie noch nicht ausreichend gelöst zu sein scheint. Auch in der Praxis wird das Thema heiß diskutiert, wobei hier oft viel einfachere Lösungen eruiert werden. Damit die Losgrößen-Rezepte in der Praxis jedoch schmecken, muss man genau verstehen, wie sie funktionieren und wo ihre Schwachpunkte liegen.
Ziele der Losgrößenverfahren
Fragen wir uns zuerst einmal, was mit der Berechnung von Losgrößen eigentlich genau gemeint ist. Im weiteren Sinne versteht man unter einem Losgrößenverfahren jede beliebige Methode zur Festlegung einer Losgröße. Genau genommen strebt man mit der Berechnung von Losgrößen jedoch ein Optimum zwischen Lagerhaltungskosten auf der einen Seite und Beschaffungskosten für die Eigenfertigung oder die Fremdbeschaffung auf der anderen Seite an. Es geht also darum, die Gesamtkosten in einem vergleichsweise kleinen Segment einer ganzheitlichen Supply Chain zu minimieren. Damit muss man nicht immer richtig liegen; das wird deutlich wenn man sich vor Augen hält, dass eine einzige Losgrößenentscheidung, beispielsweise im Einkauf oder für einen spezifischen Wertschöpfungsschritt in der Produktion, nicht zwangsläufig für das Gesamtoptimum der Supply Chain förderlich sein muss. Hierum geht es aber letztlich.
Das Gesamtoptimum nicht aus dem Auge verlieren
Interdependenzen zwischen einzelnen Gütern müssen folglich vorab spezifiziert werden, damit festgelegt werden kann, in welchem Bereich Losgrößenverfahren überhaupt sinnvoll angewandt werden können. Erst wenn dies bekannt ist und wenn für diese Interdependenzen klare Regeln erstellt worden sind, kann man sich mit den optimalen Losgrößenverfahren beschäftigen. Fangen Sie also niemals ein Losgrößenprojekt an, ohne vorher auch einen Blick auf die gesamte Supply Chain geworfen zu haben. Dass dies wichtig ist, werden Sie bereits erkennen, wenn Sie sich genauer mit den Losgrößenverfahren beschäftigen.
Welche Möglichkeiten es bei den Losgrößenverfahren gibt und welche wirklich empfehlenswert sind. Danach kommen wir zu einer Einordnung der Losgrößenverfahren innerhalb der gesamten Supply Chain Optimierung, um Anwendern abschließend klar zu machen, was sie tun, wenn sie Losgrößenverfahren anwenden und was sie zusätzlich noch beachten müssen. Halten wir an diesem Punkt also nochmals fest: Es geht nur um Kostenreduktion bei einem spezifischen Gut. Nichts anderes als Kosten für dieses spezifische Gut werden also betrachtet.
Die Grundlage aller Losgrößen-Berechnungen bildet dabei konsequenterweise die Ermittlung der relevanten Kosten.
Update 2021: für aktuelleren Beitrag diesem Link folgen
Kostenarten bei der Losgrößenoptimierung
Zwei gegenläufig reagierende Kostenarten werden bei der Losgrößenoptimierung im Allgemeinen betrachtet: Lagerhaltungskosten auf der einen und Beschaffungskosten auf der anderen Seite. Die Lagerhaltungskosten setzen sich beispielsweise aus einer ganzen Reihe von Kostenarten zusammen. Neben den Zinsen des gebundenen Kapitals gehören hierzu auch weitere Kostenarten, die oft deutlich größer ausfallen, als die Zinsen alleine. Zu nennen sind vor allem: Kosten für Alterung und Verschleiß, Verlust und Bruch, Transport und Handling innerhalb des Lagers, Lagerung und Abschreibung sowie Lagerverwaltung und Versicherung.
Auf der anderen Seite der Waagschale stehen die Beschaffungskosten der Eigen- oder Fremdfertigung. Zu diesen Kosten zählen v.a. Bestellkosten, Rabatte, Boni, Skonti, Zusatzkosten bei ungünstigen Bestell- oder Fertigungsmengen, Transport-, Versicherungs- und Verpackungskosten, Auftragsbearbeitungskosten und natürlich die Rüstkosten.
Größere Losgrößen in der Beschaffung oder der Fertigung führen zu höheren Beständen und damit höheren Lagerhaltungskosten. Diese steigen im Allgemeinen proportional zur Losgröße, während die Beschaffungskosten degressiv fallen. Das lässt sich am Beispiel der Transportkosten leicht verdeutlichen: Fallen für ein bestelltes Teil dieselben absoluten Transportkosten an, wie für zwei Teile, dann trägt bei zwei bestellten Teilen jedes nur noch die Hälfte der Transportkosten (vgl. Abb. 1).
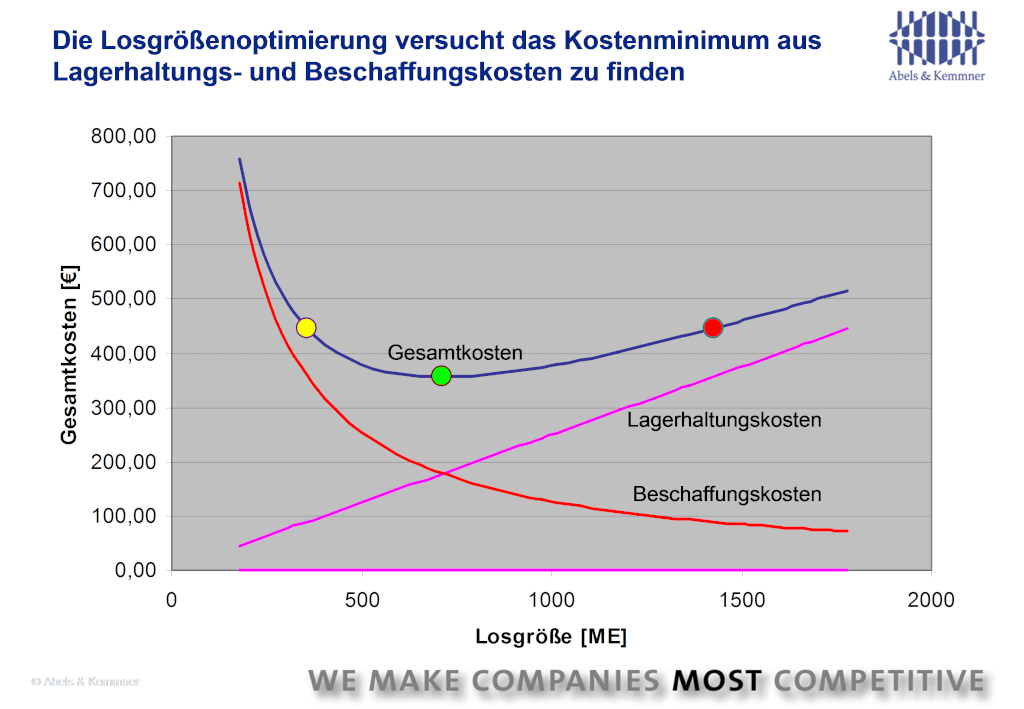
Wie bringt man nun diese unterschiedlichen Kostenkurven zu einem Gesamtoptimum? Hierzu wurden und werden noch immer unterschiedliche Verfahren entwickelt, die man in der Summe unter Losgrößenverfahren zusammenfasst.
Die wichtigsten Losgrößenverfahren
Bei den Losgrößenverfahren unterscheidet man gewöhnlich zwischen statischen Verfahren und dynamischen Verfahren. Statische Verfahren betrachten keine in der zeitlichen Abfolge variierenden Fertigungs- oder Bestellbedarfe, sondern nur die gesamte Bedarfsmenge innerhalb eines Betrachtungszeitraums und sind damit nur überschlägige Berechnungsverfahren.
Das bekannteste statische Losgrößenverfahren und wohl auch das bekannteste Losgrößenverfahren überhaupt, ist das Andler-Verfahren (Equal Order Quantity-Verfahren).
Dynamische Verfahren bzw. periodische Losgrößenverfahren betrachten hingehen über einen Zeitraum hinweg z.B. den variierenden Bedarf pro Woche und kommen so zu unterschiedlichen Losgrößen pro Woche. Darüber hinaus berechnen sie Losgrößen rollierend und sind damit grundsätzlich nachfrageorientierter und können sich so veränderten Bedarfen anpassen. Zu dieser Gruppe von Verfahren gehören:
- das Wagner-Whitin-Verfahren
- das Part-Period-Verfahren (Stück-Perioden-Ausgleichsverfahren)
- das Stückkosten-Verfahren (Verfahren der gleitenden wirtschaftlichen Losgröße)
- das Groff-Verfahren
- das Silver-Meal-Verfahren.
Der unbedarfte Leser mag sich nun fragen, ob so viele Verfahren existieren müssen? Gibt es etwa mehrere Wahrheiten? Natürlich gibt es nicht mehrere Wahrheiten, sondern nur eine. Doch diese konnte bisher niemand in einer Formel wirklich exakt abbilden, da die Sachverhalte in der Realität viel zu komplex und differenziert sind, als dass man sie in einer vergleichsweise wenig komplexen Formel oder Formelsammlung unterbringen könnte Insofern stellen alle Losgrößenverfahren nur Näherungslösungen dar. Einige sind jedoch näher am Optimum als andere. Die oben aufgeführten Verfahren muss man deshalb sehr genau verstehen, um sie nutzbringend anwenden zu können.
Damit bleibt festzuhalten – wie schon in der Headline beschrieben:
Losgrößenverfahren sind für eine ideale Welt gemacht
Alle der oben genannten Verfahren beschreiben das Zusammen- bzw. Gegeneinanderwirken von Lagerhaltungskosten und Beschaffungskosten in einer einstufigen Einprodukt-Fertigung ohne Kapazitätsbegrenzung. Eine solche liegt beispielsweise vor, wenn Sie stolzer Besitzer einer Druckmaschine sind, auf der Sie eine Druckplatte aufgespannt haben. Das Einrichten der Druckmaschine kostet Sie unabhängig von Ihrer Arbeitskraft Papier und Druckfarbe, da sie eine ganze Zeit lang Makulatur produzieren, bis Sie die Maschine richtig eingerichtet haben. Da Sie dasselbe Pamphlet immer wieder produzieren müssen, stellt sich für Sie einzig und alleine das Dilemma aus hohen Fertigungslosen und damit geringen anteiligen Rüstkosten einerseits und hohen Lagerbeständen und Bestandskosten andererseits. Die Losgrößenberechnungsformeln der klassischen Verfahren versuchen genau für diese Situation eine „Trade-off“-Formel zu beschreiben. Nicht weniger, aber auch nicht mehr.
Eigentlich tritt die Frage nach einer Losgröße jedoch erst auf, wenn mehr als ein Produkt gefertigt wird, denn solange ich nur ein Produkt auf der Anlage fertige, muss ich ja gar nicht umrüsten. Werden mehrere Produkte auf einer Anlage gefertigt, stimmen unsere Formeln auch noch, sofern sich die Losgrößen der beiden Produkte nicht gegenseitig durch eine begrenzte Maschinenkapazität beeinflussen.
Augenmerk auch für andere Kennzahlen erforderlich
Eine begrenzte Maschinenkapazität ist in der Praxis jedoch dummerweise häufig der Fall. Müssen sich mehrere Produkte diese teilen, dann lassen sich die erforderlichen Losgrößen zwar ebenfalls berechnen, doch das wirklich entscheidende Kriterium ist in diesem Falle nicht die Minimierung der Gesamtkosten, sondern die Entscheidung über die Erfüllung der Nachfragemengen. Damit sind wir bei einer sogenannten EPEI-Berechnung (Every Part Every Intervall), die mit der klassischen Losgrößenberechnung nichts mehr zu tun hat. Das Kostenoptimum weicht einer Abwägung, welche Produkte man vorrangig produziert und welche zurückgestellt oder gar nicht mehr selbst produziert werden, um so eine möglichst gewinnbringende Produktion zu gewährleisten. Sie sehen: Es gibt noch andere Aspekte, die zu einem Gesamtoptimum beitragen.
Der Einkauf muss auch übergeordnet optimieren
Nun könnte man auf den ersten Blick meinen, dass es in der Beschaffung anders aussieht. Dem ist aber nicht so. Auch hier kann häufig keine isolierte Losgrößenbetrachtung bei einem einzelnen Produkt angestellt werden. Zum einen können sich mehrere verschiedene Produkte Beschaffungskosten „teilen“: denken Sie beispielsweise an einen LKW, der mit mehreren Produkten beladen werden kann. Zum anderen geht es häufig darum, den LKW voll zu bekommen, um möglichst geringe Transportkosten zu erreichen. Mehrere Produkte werden also gezielt zusammen bestellt und beeinflussen sich somit hinsichtlich ihrer Bestellmengen gegenseitig. Mit der vermeintlich „optimalen“ Bestellmenge eines Produktes schränke ich folglich den Spielraum der Bestellmengen für die anderen Produkte automatisch ein.
Und letztlich kämpfen auch Lieferanten – entgegen der weitverbreiteten Meinung mancher Einkaufabteilungen – ebenfalls mit begrenzten Kapazitäten, womit sich verschiedene, vermeintlich unabhängige Bestellungen unterschiedlicher Produkte bei einem Lieferanten auch wiederum gegenseitig beeinflussen.
Werfen wir hierzu nochmals einen Blick in die Produktion: Was passiert eigentlich in einer Fertigung, in der ich von Fertigungsstufe zu Fertigungsstufe die Losgrößen optimiere? Beim Drehen arbeite ich mit 450 Stück im Fertigungsauftrag, beim anschließenden Fräsen habe ich 380 Stück als „optimal“ ermittelt und beim anschließenden Galvanisieren komme ich mit spitzen Bleistift zu einer Losgröße von 1250 Stück… Eine solche Optimierung verursacht zumindest einiges an Zwischenbeständen, die bei der Einzelfall-Berechnung nicht berücksichtigt worden sind. Und vielleicht muss ich sogar mehrere „optimale“ Fertigungsmengen direkt nacheinander produzieren… Sie sehen, so einfach eine Formel im Einzelfall ist, so komplex ist die Realität.
Komplexer ist exakter, aber auch schwieriger
Natürlich hat man sich in der Wissenschaft auch mit dieser Fragestellung beschäftigt. So gibt es Losgrößenoptimierungsverfahren, die eine gesamte Prozesskette berücksichtigen. Will man nun aber realistischerweise auch noch berücksichtigen, dass die Kapazitäten auf den einzelnen Fertigungsstufen begrenzt sind, lässt sich die Realität nicht mehr vollständig mit all den gegebenen Interdependenzen und Limitierungen durchrechnen; selbst Großrechner reichen hierzu noch nicht aus.
Darüber hinaus sind all diese komplexeren Verfahren für die Praxis zu kompliziert. Zumindest bis heute, denn wer kann in einem komplexen Regelwerk erkennen, an welchen Stellgrößen man drehen kann und muss, um das Ergebnis der jeweiligen Gesamtoptimumsformel auch wirklich praxistauglich zum Optimum zu führen? Deshalb versucht man heute zumeist nur mit den einfacheren Verfahren der komplizierten Realität näherzukommen und bekommt hierzu eine Reihe von Losgrößenverfahren in den ERP-Systemen bereitgestellt. Nicht jedes Verfahren ist jedoch wirklich sinnvoll. Das habe ich schon grob skizziert. Lassen Sie uns deshalb nun noch einen kleinen Blick auf einige Formeln werfen um sie konkret zu bewerten. Damit es etwas kurzweiliger wird, machen wir das am besten in einem kleinen historischen Abriss ohne Anspruch auf Vollständigkeit.
Die Geschichte der Losgrößenberechnung
Andler ist oft zu simpel
Die Idee der wirtschaftlichen Losgrößenoptimierung geht bereits in die Anfänge des letzten Jahrhunderts hinein. Der Amerikaner F.W. Harris1 war wohl der erste, der sich zu diesem Thema Gedanken gemacht hatte. 1929 entwickelte Kurt Andler eine differenziertere Formel zur Berechnung einer wirtschaftlichen Losgröße. Die Formel im Einzelnen ersparen wir uns hier. Wer sich die Mühe machen möchte, die Formel nachzuvollziehen, sei auf unzählige Quellen im Internet verwiesen. Die Andlerformel macht nichts anderes, als das Minimum der Gesamtkostenkurve in Abb. 1 zu ermitteln. Bei der Berechnung der Losgröße ging Andler davon aus, dass die Gesamtbedarfsmenge eines Artikels in einem Planungszeitraum, z.B. ein Jahr, bekannt ist. Die Formel leitet nun aus Lagerhaltungskosten einerseits und Beschaffungskosten andererseits die Losgröße ab, mit der immer wieder bestellt werden sollte. Da die Losgröße über den Planungszeitraum konstant bleibt, spricht man auch von einer statischen Losgrößenformel.
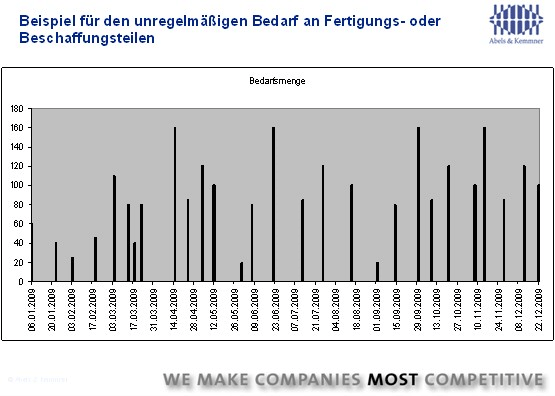
Im praktischen Leben ist es jedoch zumeist so, dass die Produktions- oder Bestellbedarfe über einen Planungszeitraum, der typischerweise kürzer als ein Jahr ist, nicht konstant sind. Sie folgen vielmehr unregelmäßig aufeinander und fallen unterschiedlich hoch aus (Abb. 2).
Die Vermutung liegt nahe, dass es in diesen Fällen eine genauere Lösung für eine wirtschaftliche Losgröße geben muss, als den Gesamtbedarf über den Betrachtungszeitraum zusammenzufassen und hieraus eine statische Losgröße zu berechnen, die nie richtig zu den voraussichtlichen Bedarfsmengen passt. Die entscheidende Antwort gaben zwei Amerikaner bereits 1958.
Wagner-Within ist sehr exakt
Die Herren Wagner und Whitin entwickelten ein Losgrößenberechnungsverfahren – mehr als nur eine einzige Formel – mit der dynamische Losgrößen berechnet werden konnten. Die elegante mathematische Lösung der beiden Herren berücksichtigt, dass mit der Entscheidung über eine erste Losgröße im Betrachtungszeitraum automatisch auch der Spielraum für die Gestaltung der zeitlich nachfolgenden Losgrößen eingeschränkt wird. Das Wagner-Whitin-Verfahren ermittelt eine Folge von Losen mit unterschiedlicher Größe und unterschiedlichen Zeitabständen so, dass die Gesamtkosten minimiert werden. Damit war bereits die wissenschaftlich präzise Antwort auf die Frage der richtigen Losgrößen bei einer einstufigen Einproduktfertigung ohne Kapazitätsbegrenzung gegeben. Das Wagner-Whitin-Verfahren lässt sich sogar mit der Hand rechnen, was allerdings zu lange dauert, um auf diese Weise Losgrößen für unzählige Produkte zu berechnen. Zwar standen bald auch Computer für Berechungsverfahren zur Verfügung, doch das Wagner-Whitin-Verfahren ist eine zu rechenaufwändige Lösung für die damals verfügbaren Großrechner mit 8 KByte Hauptspeicher. Näherungsverfahren mit einfacheren Rechenmethoden mussten deshalb her, mit denen Computer, auf Kosten der Genauigkeit, zurecht kamen. So wurde beispielsweise 1968 das Part Period-Verfahren entwickelt, 1969 das nach seinen Entwicklern genannte Silver-Meal-Verfahren und 1979 das Groff-Verfahren.
Da diese Näherungsverfahren verschiedene Vereinfachungen vornehmen, ermitteln sie das Kostenoptimum auch bei unterschiedlichen Losgrößen. Die Abweichungen vom exakt rechnenden Wagner-Whitin-Verfahren können dabei sehr deutlich ausfallen, wie Abb. 3 zeigt:
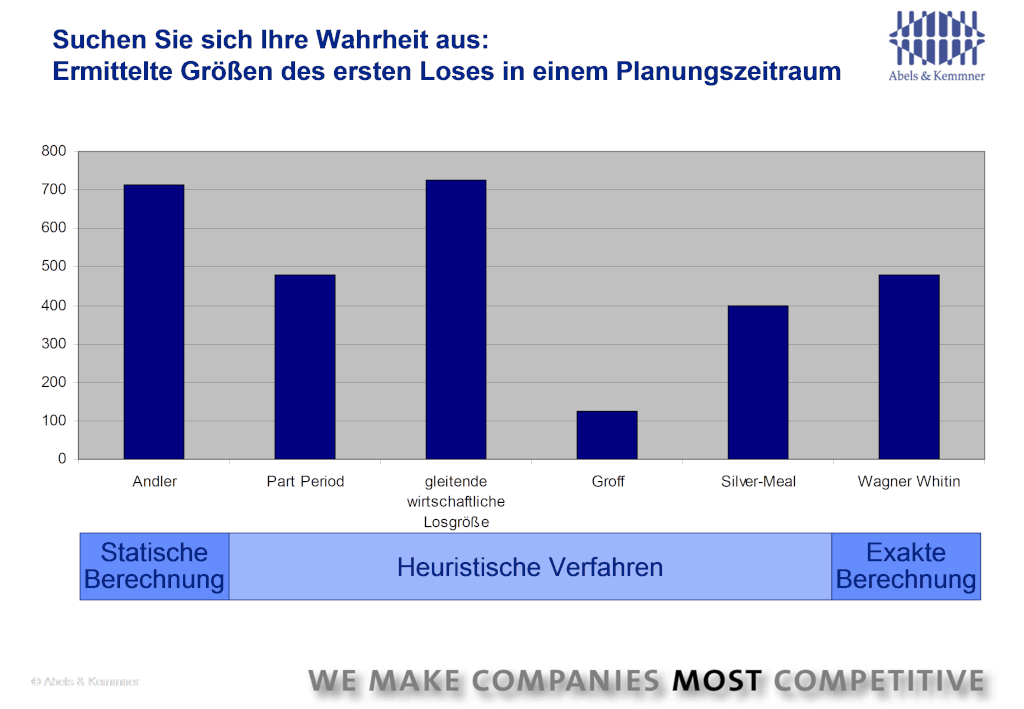
Spätestens seit Mitte der 1990er Jahre waren die Computer schnell genug geworden, um auch auf eine große Anzahl an Artikeln das Wagner-Whitin-Verfahren anwenden zu können. In den meisten heutigen Standard ERP-Systemen fehlt es jedoch weiterhin. Dafür werden in den Systemen noch immer die Andlerformel, die für bestimmte Aspekte ihre Berechtigung hat, und die heuristischen Verfahren angeboten. Die Anwender sind damit zufrieden; einerseits wohl, weil sie nicht wissen, dass es bessere Verfahren gibt und andererseits, weil man sich im Laufe der Jahre an alle diese Verfahren gewöhnt hat. Das Wagner-Whitin-Verfahren findet man derzeit zumeist nicht in ERP-Systemen. Es gibt allerdings AddOn-Systeme zur Supply Chain Optimierung, die Wagner-Whitin anbieten. Die sollten Sie sich deshalb anschauen. Wenn Sie dann soweit sind und mit Wagner-Whitin ihre optimalen Losgrößen suchen wollen, dann nun noch ein paar abschließende Hinweise:
Vermeiden Sie falsche kalkulatorische Kosten
Üblicherweise wird bei der Betrachtung der Kosten mit einem kalkulatorischen Wert jeweils für Lagerungskosten und Beschaffungskosten gearbeitet. Für Näherungsberechnungen ist dies auch sehr hilfreich. Bei differenzierterer Betrachtung aber nicht ausreichend. Schauen wir uns dies zuerst einmal am Beispiel der Beschaffungskosten an:
Vielleicht kennen Sie den Fall des Radiergummis, dessen Beschaffung 50 EUR kostet; ein Fall, der vor einigen Jahren durch die Presse geisterte, als man über die Vorteile der Beschaffung über das Internet diskutierte. Wie kommt man in einer Berechnung zu einem solchen ausgefallenen Wert für einen Cent-Artikel? Eigentlich ganz einfach: man betrachtet nicht nur den Einkaufspreis des Artikels, sondern berücksichtigt richtigerweise auch die Kosten, die für die Beschaffung des Radiergummis entstehen. Jemand schreibt vielleicht eine Anforderung, diese wird möglicherweise noch vom Vorgesetzten abgezeichnet, dann an den Einkauf weitergeleitet. Unterstellen wir einmal vereinfachend, dass der Einkauf für den Radiergummi keine drei Angebote einholt (bei manchen Einkaufsabteilungen bin ich mir hierüber allerdings nicht so sicher). Der Einkäufer bestellt, möglicherweise via SAP aus einem Rahmenvertrag, der einmal ausgehandelt werden musste, den gewünschten Radiergummi. Dazu muss er eine Bestellung anlegen und freigeben. In einem Unternehmen, das ich gut kenne, wird die Bestellung nun noch ausgedruckt, unterschrieben und dann gefaxt. Das Original der Bestellung wird in einem Ordner abgelegt. Wird der Radiergummi geliefert, geht der Prozess weiter, doch ersparen wir uns dessen Beschreibung hier.
Klar ist, dass hier „Beschaffungskosten“ entstehen, die unabhängig vom Preis der beschafften Ware sehr hoch sein können. In unserem Beispielsunternehmen fallen für den Einkauf im Unternehmen Personalkosten in Höhe von 250.000 € an. Der Kostenanteil für die IT-Software und Hardware mögen sich auf weitere 15.000 € belaufen. Nehmen wir an, dass für die restlichen Kosten nochmals 35.000 € anfallen. In Summe „kostet“ der Einkauf mit seinen Prozessen im Jahr dann 300.000€. Der Aufwand im Wareneingang beläuft sich auf nochmals 300.000 €. In Summe kostet das Bestellen und Vereinnahmen von Waren in unserem Unternehmen also 600.000€. Im Jahr fallen 11.000 Bestellungen an. Hieraus ergibt sich ein Betrag von 54,55€ pro Bestellung. So einfach ist die Rechnung – und so falsch ist sie auch!
Natürlich würde man für einen Radiergummi einen einfacheren Bestellprozess definieren, weiterhin ist klar, dass der Einkauf bei teueren Produkten mehr Zeit aufwenden würde, als bei billigen. Was würde letztlich passieren, wenn statt 11.000 Bestellungen im Jahr 15.000 Bestellungen anfallen würden, weil in kleineren Losen bestellt wird? Damit würden bei 240 Arbeitstagen im Einkauf pro Jahr ca. 62 Bestellungen pro Tag ausgelöst anstatt knapp 46 Bestellungen. Vielleicht würde der Einkauf diese Steigerung noch mit dem bestehenden Personal auffangen können. Damit wären die Kosten pro Bestellung auf einmal bei 40€!! Die Grenzkosten, d.h. die zusätzlichen Kosten für jede weitere Bestellung lagen hiermit bei 0 Euro. Berücksichtigt man Bestellkosten bei der Losgrößenoptimierung, interessieren eigentlich nur die variablen Kosten, die wirklich bei jeder Bestellung neu anfallen. Die fixen Kostenanteile sind „Eh-da-Kosten“, die bei der Losgrößenoptimierung erst für die Entscheidung relevant werden, wenn sie durch die erhöhte Zahl von Beschaffungsvorgängen erhöht werden.
Selbst bei Kostenpositionen, die vermeintlich wirklich bei jeder Lieferung anfallen, kann dieser Grenzkosteneffekt auftreten. Nehmen wir an, jede Lieferung seitens des Büromaterialhandels kostet Frachtkosten in Höhe von 5€. Wäre der Radiergummi heute die einzige Bestellung bei dem Büromateriallieferanten, dann wären die 5€ den Beschaffungskosten des Radierers hinzuzuzählen. Vermutlich wird aber jeden Tag sowieso eine ganze Menge an Büromaterial geliefert. Der Frachtkostenanteil des Radierers beträgt also zumindest nur ein Bruchteil der 5€. Ob heute ein Teil mehr oder weniger vom Büromateriallieferanten geliefert wird, schlägt sich in den Frachtkosten nicht nieder. Die Grenzkosten sind also wiederum Null.
Betrachten wir die Rüstkosten in der Fertigung, gilt entsprechendes. Viele Unternehmen berechnen Rüstkosten als Maschinenstundensatz multipliziert mit der Rüstzeit. Habe ich bei jedem Rüstvorgang Anlaufverluste, wie beispielsweise beim Andrucken eines neu eingerüsteten Druckauftrages, muss ich diese Kosten bei den Rüstkosten mitbetrachten. Fallen solche Kosten nicht an und ist meine Fertigungskapazität ausreichend, wie dies an vielen Nicht-Engpass-Arbeitsplätzen der Fall ist, rüstet mein Bedienpersonal die Maschine selbst und kann ich das Personal nicht einfach an andere Arbeitsplätze versetzen oder nach Hause senden, wenn nichts zu tun ist, dann sind die Grenzkosten des Rüstens wiederum null. Anstatt die Produktion auf der Maschine anzuhalten und die Leute pausieren zu lassen, weil nichts mehr zu tun ist, kann ich sie auch ihre Zeit damit verbringen lassen, häufiger zu rüsten. Mit pauschalen „Set-up“-Kosten bei der Berechnung der Fertigungslose berücksichtigen wir diesen Effekt überhaupt nicht.
Was zum Schluss bleibt
Je genauer man hinsieht, desto mehr Ungenauigkeiten findet man in der Praxis bei der Berechnung von Losgrößen. Die Losgrößenberechnung ist deshalb jedoch nicht tot. Sie hat gerade in der heutigen Zeit, in der es darum geht, die Supply Chains und Wertschöpfungsketten so schlank wie möglich zu gestalten ihre Berechtigung. Um zu sinnvollen Losgrößenberechnungen zu gelangen, muss man die einzelnen Verfahren, geltenden Randbedingungen und Vereinfachungen jedoch sehr genau verstehen. Losgrößenoptimierung ist somit doch nicht die einfache Supply Chain Optimierung mittels Formelsätzen, die man einfach im PC berechnen lässt, sondern ein Optimierungsansatz für Spezialisten, die zunächst die Anwendung der Methode in den richtigen Kontext setzen und dann auch die Kostenberechnungen so einstellen, dass sie ausreichend genau sind. Alles andere ist ein Stochern im Nebel.
1 Harris, F.W.: How Many Parts to Make at Once Factory: The Magazine of Management 10(2): 135-136,152 (1913)

