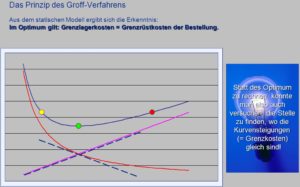
Das 1979 publizierte Losgrößen-Verfahren nach Groff ist eine Weiterentwicklung des Andler-Verfahrens und geht von der Erkenntnis aus, dass das Minimum der Gesamtkosten aus Lagerhaltungskosten einerseits und Rüstkosten andererseits dort liegt, wo die Grenz-Rüstkosten den Grenz-Lagerkosten entsprechen.
Die Rüstkosten in der Produktion können Sie senken, indem Sie die produzierten Losgrößen erhöhen. Das bedeutet aber, dass Sie Roh- und Fertigwarenbestände erhöhen müssen – was höhere Lagerhaltungskosten verursacht. Wie mit allen Verfahren zur Berechnung einer wirtschaftlichen Losgröße, balancieren Sie auch mit dem Groff-Verfahren gewissermaßen die Losgröße gegen Lagerhaltungs- und Rüstkosten aus, so dass Ihnen die geringstmöglichen Gesamtkosten entstehen (siehe Grafik).
Um das Verfahren anwenden zu können, müssen Sie folgende Parameter kennen:
- die Rüstkosten k (Euro/Los),
- die Lagerhaltungskosten h (Euro/Stück/Periode)
- den Bedarf B der nächsten Perioden (Tage, Wochen) und
- die kommenden Perioden n.
In einer Formel ausgedrückt, lässt sich die optimale Losgröße daher so darstellen:
Lopt = Bt+n * n * (n+1) ≤ (2*k) / h; der Faktor (n+1) ist dabei die Anzahl der Perioden im Los.
Sobald diese Bedingung nicht mehr erfüllt ist, überschreitet die Losgröße das Optimum.
Wie das Part-Period-Verfahren, oder das Verfahren der gleitenden wirtschaftlichen Losgröße, stellt auch das Groff-Verfahren ein Näherungsverfahren zur Optimierung der Losgrößen dar.
Unser Tipp: Präziser als das Groff-Verfahren rechnet der Wagner-Whitin-Algorithmus. Dieser ist rechentechnisch zwar deutlich aufwändiger, dies spielt bei heutigen Leistungsfähigkeit der Computer aber keine Rolle mehr.
Bild: iStock

