Using theoretical formulas to optimize costs in practice?
At first glance, lot-sizing methods for reducing the overall costs of warehousing and procurement of a particular good appear very interesting. However, in order to fully exploit the potential, users must also be aware of the limitations of lot-sizing methods and be aware that they cannot take into account all interdependencies throughout the company. The right methodological expertise is therefore required across the entire supply chain to ensure that it is used at the right strategic point.
Hardly any other topic has been the subject of as many dissertations as batch size optimization. And new concepts and dissertations on batch size calculation are still appearing, which at least shows that the optimization of batch sizes does not yet seem to have been sufficiently solved in theory. The topic is also hotly debated in practice, although much simpler solutions are often found here. However, for the batch size recipes to work in practice, you need to understand exactly how they work and where their weak points lie.
Objectives of lot-sizing procedures
Let us first ask ourselves what exactly is meant by the calculation of batch sizes. In a broader sense, a lot-sizing procedure is any method for determining a lot size. Strictly speaking, however, the calculation of batch sizes aims to achieve an optimum between inventory costs on the one hand and procurement costs for in-house production or external procurement on the other. The aim is therefore to minimize overall costs in a comparatively small segment of a holistic supply chain. You don’t always have to be right; this becomes clear when you consider that a single batch size decision, for example in purchasing or for a specific value-added step in production, does not necessarily have to be conducive to the overall optimum of the supply chain. But that is ultimately the point.
Don’t lose sight of the overall optimum
Interdependencies between individual goods must therefore be specified in advance so that it can be determined in which area lot-sizing procedures can be applied at all. Only when this is known and clear rules have been drawn up for these interdependencies can the optimum lot-sizing process be considered. So never start a batch size project without first taking a look at the entire supply chain. You will realize that this is important as soon as you take a closer look at the lot-sizing process.
What options are available for lot-sizing processes and which are really recommended. We then move on to a classification of lot-sizing methods within the overall supply chain optimization in order to make it clear to users what they are doing when they use lot-sizing methods and what else they need to consider. So let’s reiterate at this point: it’s all about reducing the cost of a specific good. Nothing other than costs for this specific good are therefore considered.
The basis of all batch size calculations is consequently the determination of the relevant costs.
Update 2021: follow this link for a more up-to-date article
Cost types for lot size optimization
Two opposing cost types are generally considered in lot size optimization: Inventory costs on the one hand and procurement costs on the other. Warehousing costs, for example, are made up of a whole range of cost types. In addition to the interest on the tied-up capital, this also includes other types of costs that are often significantly higher than the interest alone. These include, in particular, costs for aging and wear, loss and breakage, transportation and handling within the warehouse, storage and depreciation, as well as warehouse management and insurance.
On the other side of the scales are the procurement costs of in-house or external production. These costs include, above all, ordering costs, rebates, bonuses, discounts, additional costs for unfavorable order or production quantities, transport, insurance and packaging costs, order processing costs and, of course, set-up costs.
Larger batch sizes in procurement or production lead to higher inventories and therefore higher warehousing costs. These generally increase in proportion to the batch size, while procurement costs fall degressively. This can be easily illustrated using the example of transportation costs: If the same absolute transportation costs are incurred for one ordered part as for two parts, then if two parts are ordered, each part only bears half of the transportation costs (see Fig. 1).
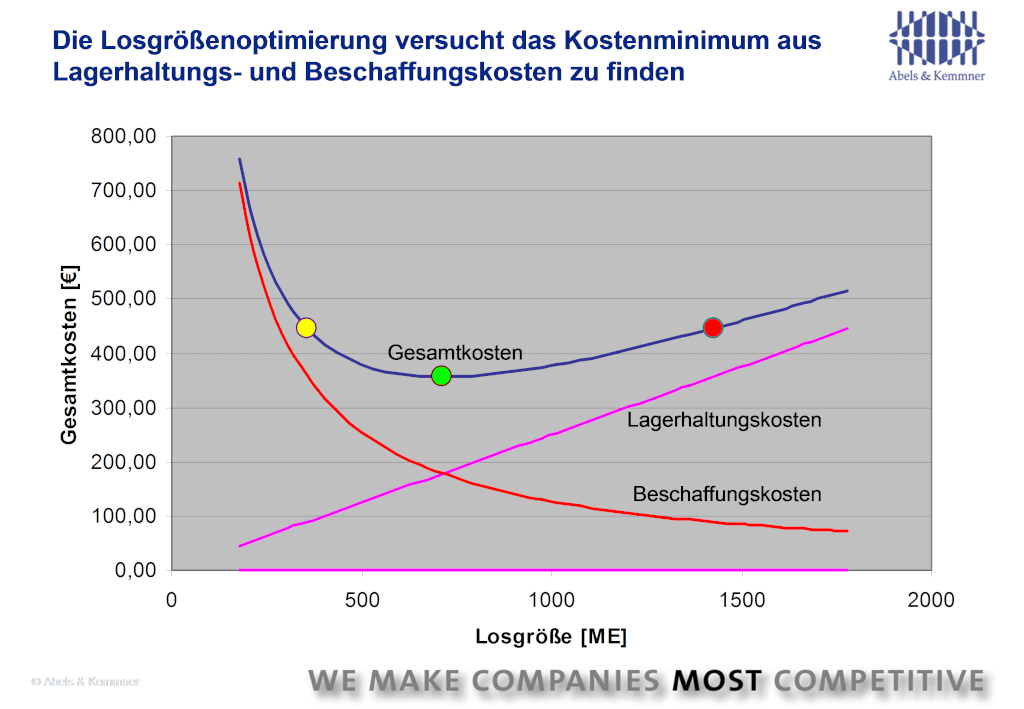
How can these different cost curves be brought to an overall optimum? Various procedures have been and are still being developed for this purpose, which are summarized under batch size procedures.
The most important lot-sizing methods
With lot-sizing methods, a distinction is usually made between static methods and dynamic methods. Static methods do not consider production or order requirements that vary over time, but only the total quantity required within an observation period and are therefore only approximate calculation methods.
The best-known static lot-sizing method, and probably the best-known lot-sizing method of all, is the Andler method (equal order quantity method).
Dynamic methods or periodic lot-sizing methods consider, for example, the varying demand per week over a period of time and thus arrive at different lot sizes per week. In addition, they calculate batch sizes on a rolling basis and are therefore fundamentally more demand-oriented and can thus adapt to changing requirements. This group of procedures includes
- the Wagner-Whitin method
- the part-period method (piece-period equalization method)
- the unit cost method (sliding economic lot size method)
- the Groff process
- the Silver Meal process.
The inexperienced reader may now ask whether so many procedures need to exist? Are there several truths? Of course, there are not several truths, but only one. However, no one has yet been able to map these exactly in a formula, as the facts in reality are far too complex and differentiated to be accommodated in a comparatively less complex formula or collection of formulas. However, some are closer to the optimum than others. The procedures listed above must therefore be understood very precisely in order to be able to use them effectively.
As already described in the headline, it remains to be said:
Batch sizing processes are made for an ideal world
All of the above methods describe the interaction or counteraction of inventory costs and procurement costs in a single-stage, single-product production process without capacity limits. This is the case, for example, if you are the proud owner of a printing press on which you have mounted a printing plate. Setting up the press will cost you paper and ink regardless of your labor, as you will be producing waste for quite some time until you have set up the press correctly. As you have to produce the same pamphlet over and over again, the only dilemma you face is that of high production batches and therefore low pro rata set-up costs on the one hand and high stock levels and inventory costs on the other. The batch size calculation formulas of the classic methods attempt to describe a “trade-off” formula for precisely this situation. No less, but also no more.
However, the question of a batch size only really arises when more than one product is manufactured, because as long as I only manufacture one product on the system, I don’t have to retool at all. If several products are manufactured on one system, our formulas are still correct as long as the batch sizes of the two products do not influence each other due to limited machine capacity.
Attention also required for other key figures
However, limited machine capacity is unfortunately often the case in practice. If several products have to share these, then the required batch sizes can also be calculated, but the really decisive criterion in this case is not the minimization of the total costs, but the decision on the fulfillment of the demand quantities. This brings us to a so-called EPEI calculation(Every Part Every Interval), which no longer has anything to do with the classic batch size calculation. The cost optimum gives way to a consideration of which products to prioritize and which to postpone or no longer produce in order to ensure the most profitable production possible. As you can see: There are other aspects that contribute to an overall optimum.
Purchasing must also optimize at a higher level
At first glance, you might think that things look different in procurement. But that is not the case. Here, too, it is often not possible to make an isolated batch size analysis for a single product. On the one hand, several different products can “share” procurement costs: think, for example, of a truck that can be loaded with several products. On the other hand, it is often a matter of getting the truck full in order to achieve the lowest possible transport costs. Several products are therefore ordered together and thus influence each other with regard to their order quantities. With the supposedly “optimal” order quantity for one product, I automatically limit the scope of order quantities for the other products.
And finally, suppliers – contrary to the widespread opinion of some purchasing departments – are also struggling with limited capacities, which means that different, supposedly independent orders for different products from one supplier also influence each other.
Let’s take another look at production: What actually happens in a production process in which I optimize batch sizes from one production stage to the next? For turning, I work with 450 pieces in the production order, for subsequent milling I have determined 380 pieces as “optimal” and for subsequent electroplating I arrive at a batch size of 1250 pieces with a sharp pencil… Such an optimization causes at least some intermediate stocks that have not been taken into account in the individual case calculation. And I may even have to produce several “optimum” production quantities in direct succession… As you can see, as simple as a formula is in individual cases, reality is just as complex.
More complex is more precise, but also more difficult
Of course, scientists have also looked into this issue. For example, there are batch size optimization methods that take the entire process chain into account. However, if you now also realistically want to take into account the fact that capacities at the individual production stages are limited, it is no longer possible to fully calculate reality with all the given interdependencies and limitations; even mainframe computers are not yet sufficient for this.
Furthermore, all these more complex procedures are too complicated for practical use. At least until today, because who can recognize in a complex set of rules which variables can and must be adjusted in order to achieve the optimum result of the respective overall optimum formula in a practical way? For this reason, most companies today only try to get closer to the complicated reality with the simpler procedures and are provided with a range of batch size procedures in the ERP systems. However, not every procedure really makes sense. I have already roughly sketched that out. Let us therefore now take a brief look at some formulas in order to evaluate them specifically. To make things a little more entertaining, we’ll do this in a brief historical outline without claiming to be exhaustive.
The history of batch size calculation
Andler is often too simple
The idea of economic batch size optimization dates back to the beginning of the last century. The American F.W. Harris1 was probably the first to think about this topic. In 1929, Kurt Andler developed a more sophisticated formula for calculating an economic batch size. We will spare you the details of the formula here. If you want to take the trouble to understand the formula, there are countless sources on the Internet. The Andler formula does nothing other than calculate the minimum of the total cost curve in Fig. 1 to be determined. When calculating the batch size, Andler assumed that the total quantity required of an item in a planning period, e.g. one year, is known. The formula now derives the batch size that should always be used for ordering from inventory costs on the one hand and procurement costs on the other. As the lot size remains constant over the planning period, this is also referred to as a static lot size formula.
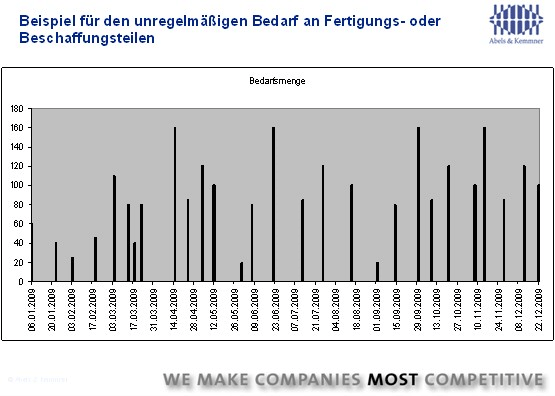
In practice, however, it is usually the case that production or order requirements are not constant over a planning period that is typically shorter than one year. Instead, they follow each other irregularly and vary in height (Fig. 2).
It is reasonable to assume that in these cases there must be a more accurate solution for an economical batch size than summarizing the total requirements over the period under consideration and calculating a static batch size from this, which never really matches the anticipated requirement quantities. Two Americans provided the decisive answer back in 1958.
Wagner-Within is very precise
Mr. Wagner and Mr. Whitin developed a batch size calculation method – more than just a single formula – with which dynamic batch sizes could be calculated. The elegant mathematical solution of the two gentlemen takes into account that the decision on a first batch size in the period under consideration automatically limits the scope for the design of the subsequent batch sizes. The Wagner-Whitin method determines a sequence of lots with different sizes and different time intervals in such a way that the total costs are minimized. This provided a scientifically precise answer to the question of the correct batch sizes for single-stage, single-product production without capacity limits. The Wagner-Whitin method can even be calculated by hand, but this takes too long to calculate batch sizes for countless products in this way. Although computers were soon available for calculation methods, the Wagner-Whitin method was too computationally complex for the mainframe computers with 8 KB of main memory available at the time. Approximation methods with simpler calculation methods were therefore needed, which computers could cope with at the expense of accuracy. For example, the part period method was developed in 1968, the Silver-Meal method named after its developers in 1969 and the Groff method in 1979.
As these approximation methods make various simplifications, they also determine the optimum cost for different batch sizes. The deviations from the precisely calculated Wagner-Whitin method can be very significant, as shown in Fig. 3 shows:
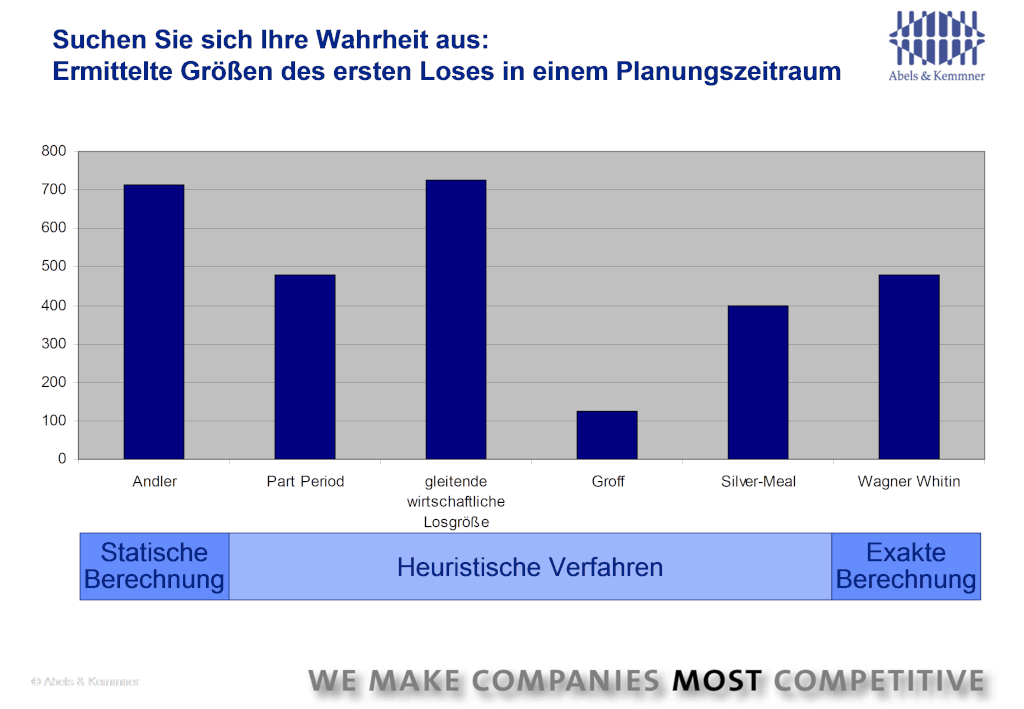
By the mid-1990s at the latest, computers had become fast enough to be able to apply the Wagner-Whitin method to a large number of articles. However, it is still missing in most of today’s standard ERP systems. The systems still offer the Andler formula, which is justified for certain aspects, and heuristic procedures. Users are satisfied with this, partly because they don’t know that there are better methods and partly because they have become accustomed to all these methods over the years. The Wagner-Whitin process is currently not usually found in ERP systems. However, there are add-on systems for supply chain optimization that Wagner-Whitin offers. You should therefore take a look at them. If you are ready to search for your optimum batch sizes with Wagner-Whitin, here are a few final tips:
Avoid incorrect imputed costs
When considering costs, an imputed value is usually used for both storage costs and procurement costs. This is also very helpful for approximate calculations. On closer inspection, however, this is not enough. Let’s first take a look at this using the example of procurement costs:
You may be familiar with the case of the eraser that costs EUR 50 to buy, a case that was in the press a few years ago when people were discussing the advantages of buying over the Internet. How do you arrive at such an unusual value for a cent item in a calculation? It’s actually quite simple: you don’t just look at the purchase price of the item, but also correctly take into account the costs incurred for procuring the eraser. Someone may write a requirement, which may be signed off by the line manager and then forwarded to the purchasing department. Let’s assume for the sake of simplicity that the purchasing department doesn’t ask for three quotes for the eraser (although I’m not so sure about this in some purchasing departments). The purchaser orders the desired eraser, possibly via SAP from a framework agreement that had to be negotiated once. To do this, he must create and release a purchase order. In one company I know well, the order is printed out, signed and then faxed. The original order is filed in a folder. If the eraser is supplied, the process continues, but we will not describe it here.
It is clear that “procurement costs” arise here, which can be very high regardless of the price of the procured goods. In our example company, personnel costs of € 250,000 are incurred for purchasing in the company. The cost share for the IT software and hardware may amount to a further €15,000. Let’s assume that another €35,000 is incurred for the remaining costs. In total, purchasing and its processes “cost” €300,000 per year. The cost of incoming goods amounts to a further € 300,000. In total, ordering and receiving goods costs our company €600,000. There are 11,000 orders a year. This results in an amount of €54.55 per order. The calculation is that simple – and that’s how wrong it is!
Of course, a simpler ordering process would be defined for an eraser, and it is also clear that purchasing more expensive products would take more time than cheaper ones. What would ultimately happen if instead of 11,000 orders a year, 15,000 orders were placed because orders were placed in smaller batches? With 240 working days in purchasing per year, this would trigger around 62 orders per day instead of just under 46 orders. Perhaps the purchasing department would still be able to absorb this increase with the existing staff. This would bring the cost per order to €40 in one go!!! The marginal costs, i.e. the additional costs for each further order, were therefore 0 euros. If order costs are taken into account in batch size optimization, only the variable costs that are actually incurred for each new order are of interest. The fixed cost components are “Eh-da costs”, which only become relevant for the decision in lot size optimization when they are increased by the increased number of procurement processes.
This marginal cost effect can even occur with cost items that are supposedly incurred with every delivery. Let’s assume that each delivery from the office supplies retailer costs €5 for freight. If the eraser were the only order placed with the office supplies supplier today, then the €5 would have to be added to the procurement costs of the eraser. But presumably a lot of office supplies are delivered every day anyway. The freight costs for the eraser are therefore at least only a fraction of the €5. Whether a part is supplied more or less by the office materials supplier today is not reflected in the freight costs. The marginal costs are therefore again zero.
If we look at the set-up costs in production, the same applies. Many companies calculate set-up costs as the hourly machine rate multiplied by the set-up time. If I have start-up losses with every makeready process, such as when printing a newly set-up print job, I have to include these costs in the makeready costs. If such costs are not incurred and my production capacity is sufficient, as is the case at many non-bottleneck workplaces, my operating personnel set up the machine themselves and I cannot simply transfer the personnel to other workplaces or send them home when there is nothing to do, then the marginal costs of setting up are again zero. Instead of stopping production on the machine and letting people pause because there is nothing more to do, I can also let them spend their time setting up more often. We do not take this effect into account at all with flat-rate “set-up” costs when calculating production batches.
What remains at the end
The closer you look, the more inaccuracies you find in practice when calculating batch sizes. However, the batch size calculation is not dead. It is particularly justified in today’s world, where the aim is to make supply chains and value chains as lean as possible. However, in order to arrive at meaningful batch size calculations, it is necessary to understand the individual procedures, applicable boundary conditions and simplifications very precisely. Batch size optimization is therefore not simple supply chain optimization using formulas that can simply be calculated on a PC, but an optimization approach for specialists who first put the application of the method in the right context and then adjust the cost calculations so that they are sufficiently accurate. Anything else is just poking around in the fog.
1 Harris, F.W.: How Many Parts to Make at Once Factory: The Magazine of Management 10(2): 135-136,152 (1913)

