The lot-sizing method according to Groff, published in 1979, is a further development of the Andler method and is based on the insight that the minimum of the total costs from inventory costs on the one hand and setup costs on the other is where the marginal setup costs correspond to the marginal inventory costs.
You can reduce set-up costs in production by increasing the batch sizes produced. However, this means that you have to increase your stocks of raw materials and finished goods – which results in higher warehousing costs. As with all methods for calculating an economical batch size, you also use the Groff method to balance the batch size against storage and set-up costs, so that you have the lowest possible total costs (see diagram).
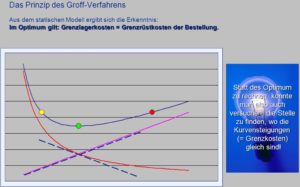
To be able to use the procedure, you need to know the following parameters:
- the set-up costs k (Euro/lot),
- the storage costs h (Euro/unit/period)
- the requirement B for the next periods (days, weeks) and
- the coming periods n.
Expressed in a formula, the optimum batch size can therefore be represented as follows:
Lopt = Bt+n * n * (n+1) ≤ (2*k) / h; the factor (n+1) is the number of periods in the batch.
As soon as this condition is no longer met, the batch size exceeds the optimum.
Like the part-period method or the sliding economic lot size method, the Groff method is also an approximation method for optimizing lot sizes.
Our tip: The Wagner-Whitin algorithm calculates more precisely than the Groff method. Although this is considerably more complex in terms of computing technology, this no longer plays a role with today’s computer performance.
Picture: iStock

